写在前面:
关于奇数阶拉丁方平衡的计算方法是个人的一点理解,如果您了解这部分的话欢迎与我探讨!您可以通过首页目标单、文章底部的评论或者邮件(charlie-techblog@outlook.com)联系到我!
其他软件操作的部分是不会错误的,Charlie很自信 :D
1. 拉丁方设计
拉丁方设计,是为了减少实验材料顺序对实验结果的影响而进行的一种平衡设计。
例如,实验材料有四个水平ABCD。我希望被试在进行全部四个水平的材料的时候,ABCD四个水平互相之间的前后出现次数是相同的,以保证实验数据不会因为四个水平材料的进行顺序而受到影响。
所以我构建了一个拉丁方矩阵:
| Block_1 | Block_2 | Block_3 | Block_4 | |
|---|---|---|---|---|
| 被试_1 | A | B | D | C |
| 被试_2 | B | C | A | D |
| 被试_3 | C | D | B | A |
| 被试_4 | D | A | C | B |
可以看到,上表中A在BCD前面的次数都是1,B在ACD的前面都是1,C在ABD前面的次数都是1,D在ABC前面的次数也都是1。
1.1 拉丁方公式
拉丁方矩阵的计算分奇数和偶数两种计算方法。但都是基于下面的公式来计算的:
1, 2, n, 3, n-1, 4, n-2
第一行根据元素个数,即材料的水平数量计算,后面逐行加1,直至形成矩阵。
首先以偶数为例,4个水平,即首行为:1,2,4,3。后面逐行加1,形成4x4拉丁方矩阵:
| 1 | 2 | 4 | 3 |
| 2 | 3 | 1 | 4 |
| 3 | 4 | 2 | 1 |
| 4 | 1 | 3 | 2 |
而奇数的计算方式则略有区别,以5个水平为例。首先我们还是根据公式形成一个拉丁方矩阵:
| 1 | 2 | 5 | 3 | 4 |
| 2 | 3 | 1 | 4 | 5 |
| 3 | 4 | 2 | 5 | 1 |
| 4 | 5 | 3 | 1 | 2 |
| 5 | 1 | 4 | 2 | 3 |
这时候其实可以注意到,上面的矩阵平不是平衡的,因此我们在这个矩阵下面补充一个左右对掉的相反矩阵来凑成平衡,最终结果是一个10x5的拉丁方矩阵:
| 1 | 2 | 5 | 3 | 4 |
| 2 | 3 | 1 | 4 | 5 |
| 3 | 4 | 2 | 5 | 1 |
| 4 | 5 | 3 | 1 | 2 |
| 5 | 1 | 4 | 2 | 3 |
| 4 | 3 | 5 | 2 | 1 |
| 5 | 4 | 1 | 3 | 2 |
| 1 | 5 | 2 | 4 | 3 |
| 2 | 1 | 3 | 5 | 4 |
| 3 | 2 | 4 | 1 | 5 |
常用的有3-6阶拉丁方设计,在此列出拉丁方矩阵方便大家使用:
3阶拉丁方矩阵
| Block_1 | Block_2 | Block_3 | |
|---|---|---|---|
| 被试_1 | A | B | C |
| 被试_2 | B | C | A |
| 被试_3 | C | A | B |
| 被试_4 | C | B | A |
| 被试_5 | A | C | B |
| 被试_6 | B | A | C |
4阶拉丁方矩阵
| Block_1 | Block_2 | Block_3 | Block_4 | |
|---|---|---|---|---|
| 被试_1 | A | B | D | C |
| 被试_2 | B | C | A | D |
| 被试_3 | C | D | B | A |
| 被试_4 | D | A | C | B |
5阶拉丁方矩阵
| Block_1 | Block_2 | Block_3 | Block_4 | Block_5 | |
|---|---|---|---|---|---|
| 被试_1 | A | B | E | C | D |
| 被试_2 | B | C | A | D | E |
| 被试_3 | C | D | B | E | A |
| 被试_4 | D | E | C | A | B |
| 被试_5 | E | A | D | B | C |
| 被试_6 | D | C | E | B | A |
| 被试_7 | E | D | A | C | B |
| 被试_8 | A | E | B | D | C |
| 被试_9 | B | A | C | E | D |
| 被试_10 | C | B | D | A | E |
6阶拉丁方矩阵
| Block_1 | Block_2 | Block_3 | Block_4 | Block_5 | Block_6 | |
|---|---|---|---|---|---|---|
| 被试_1 | A | B | F | C | E | D |
| 被试_2 | B | C | A | D | F | E |
| 被试_3 | C | D | B | E | A | F |
| 被试_4 | D | E | C | F | B | A |
| 被试_5 | E | F | D | A | C | B |
| 被试_6 | F | A | E | B | D | C |
2. 在EB中实现
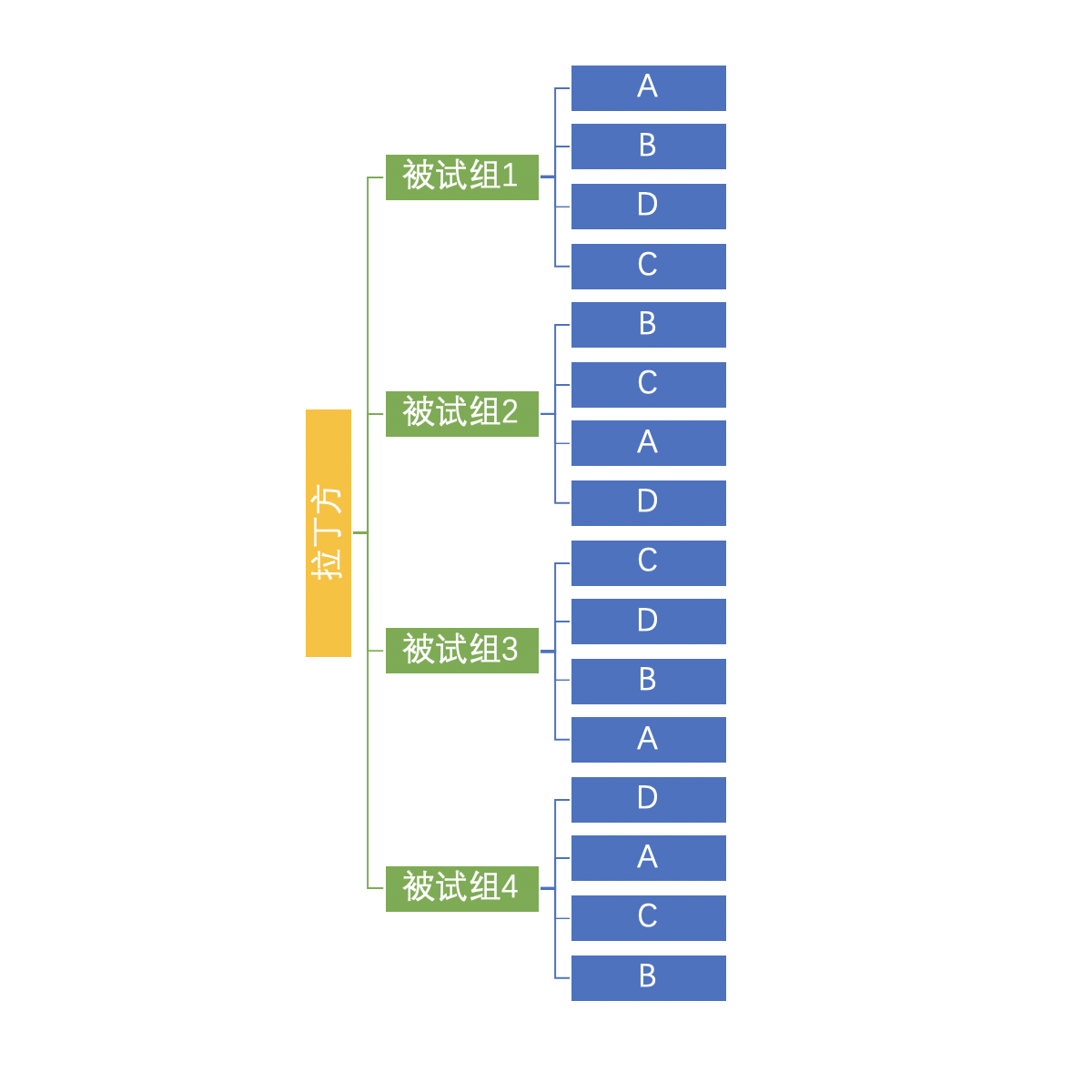
为了简化操作,方便讲解,我们以4阶拉丁方设计为例。每个水平有5个试次,4x5共计20个试次。
2.1 准备DataSource
| Latin_Group | Level | Trial_ID | Trial_Detials |
|---|---|---|---|
| 1 | A | 1 | …… |
| 1 | A | 2 | …… |
| 1 | A | 3 | …… |
| 1 | A | 4 | …… |
| 1 | A | 5 | …… |
| 1 | B | 6 | …… |
| 1 | B | 7 | …… |
| 1 | B | 8 | …… |
| 1 | B | 9 | …… |
| 1 | B | 10 | …… |
| 1 | D | 16 | …… |
| 1 | D | 17 | …… |
| 1 | D | 18 | …… |
| 1 | D | 19 | …… |
| 1 | D | 20 | …… |
| 1 | C | 11 | …… |
| 1 | C | 12 | …… |
| 1 | C | 13 | …… |
| 1 | C | 14 | …… |
| 1 | C | 15 | …… |
| 2 | B | 6 | …… |
| 2 | B | 7 | …… |
| 2 | B | 8 | …… |
| 2 | B | 9 | …… |
| 2 | B | 10 | …… |
| 2 | C | 11 | …… |
| 2 | C | 12 | …… |
| 2 | C | 13 | …… |
| 2 | C | 14 | …… |
| 2 | C | 15 | …… |
| 2 | A | 1 | …… |
| 2 | A | 2 | …… |
| 2 | A | 3 | …… |
| 2 | A | 4 | …… |
| 2 | A | 5 | …… |
| 2 | D | 16 | …… |
| 2 | D | 17 | …… |
| 2 | D | 18 | …… |
| 2 | D | 19 | …… |
| 2 | D | 20 | …… |
| 3 | C | 11 | …… |
| 3 | C | 12 | …… |
| 3 | C | 13 | …… |
| 3 | C | 14 | …… |
| 3 | C | 15 | …… |
| 3 | D | 16 | …… |
| 3 | D | 17 | …… |
| 3 | D | 18 | …… |
| 3 | D | 19 | …… |
| 3 | D | 20 | …… |
| 3 | B | 6 | …… |
| 3 | B | 7 | …… |
| 3 | B | 8 | …… |
| 3 | B | 9 | …… |
| 3 | B | 10 | …… |
| 3 | A | 1 | …… |
| 3 | A | 2 | …… |
| 3 | A | 3 | …… |
| 3 | A | 4 | …… |
| 3 | A | 5 | …… |
| 4 | D | 16 | …… |
| 4 | D | 17 | …… |
| 4 | D | 18 | …… |
| 4 | D | 19 | …… |
| 4 | D | 20 | …… |
| 4 | A | 1 | …… |
| 4 | A | 2 | …… |
| 4 | A | 3 | …… |
| 4 | A | 4 | …… |
| 4 | A | 5 | …… |
| 4 | C | 11 | …… |
| 4 | C | 12 | …… |
| 4 | C | 13 | …… |
| 4 | C | 14 | …… |
| 4 | C | 15 | …… |
| 4 | B | 6 | …… |
| 4 | B | 7 | …… |
| 4 | B | 8 | …… |
| 4 | B | 9 | …… |
| 4 | B | 10 | …… |
我们可以看到四组中ABCD的顺序是进行了拉丁方设计平衡的。
可以注意到Trial_ID的属性会根据ABCD的四种水平变换,即仍旧保持对每一个情况的试次单独做编号,方便数据处理时统计数据。
2.2 设置Datasource
首先我们到Datasource中打开Randomization Setting。
我们需要执行三个设置:
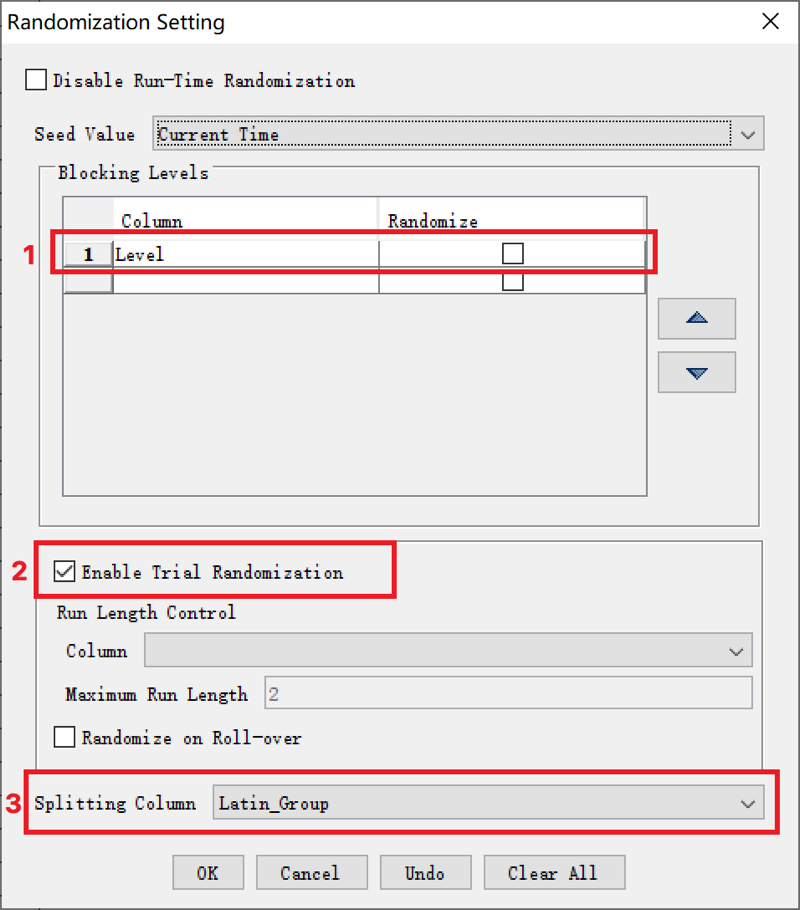
- 将Blocking_Level设置为”Level”,即每个被试在进行实验的时候会根据“Level”中的ABCD分割成四个Block。
- “Enable Trial Randomization”,开启在每个Block内的试次顺序随机。
- 最后,根据“Latin_Group”中的1234四个值将一个实验程序分割成四个,即对应四组被试实现拉丁方平衡。
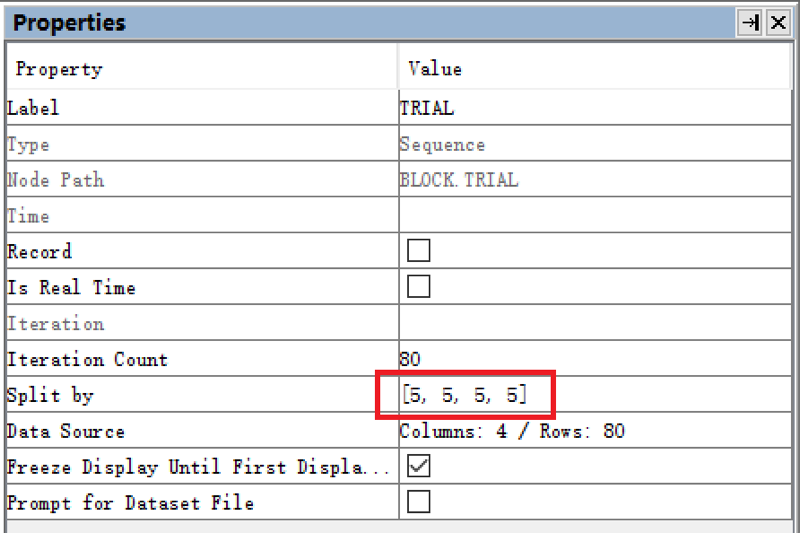
2.3 设置分割Trial执行次数
最后再设置Trial层的Split by属性为”[5, 5, 5, 5]”。即每个被试在进行实验时,运行的四个Block中,每个Block都是5个试次。
以上。